动态规划多用于以时间为单位划分阶段的动态优化过程问题，思路和分治法相似，都是将大问题划分为多个子问题。通过解决子问题的关联问题，算出动态规划的转换方程式。

原理

以斐波那契类问题为例。 爬楼梯问题：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

本题按照动态规划的思路来展示。 首先要将爬完楼梯这个问题，划分为多个子问题。 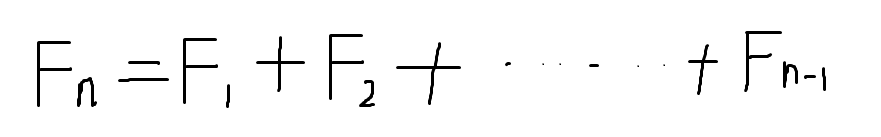将每一次抬腿看成一次子问题，则所有的抬腿动作完成后，它的总和就是本次楼梯问题的总和。 当我们有 3 阶楼梯时： 划分的子问题为：爬前两阶楼梯的方法F2+爬最后一阶楼梯的方法。 F3=F(2)+F(1) 所以对于任一阶楼梯来说，当我们需要爬到最后一阶楼梯时，他的方法总和一定是： 爬到倒数第二阶的方法+爬到倒数第一阶的方法。

                                  F(N)=F(N-2)+F(N-1)

这就是动态转换方程式，子问题向多个子问题聚合的公式。 所以动态规划的问题解决方式和分治法很相似。 都以划分子问题过程为核心，寻找转移方程以边界条件

1. 划分阶段：按照问题的时间或空间特征，把问题分为若干个阶段。在划分阶段时，注意划分后的阶段一定要是有序的或者是可排序的，否则问题就无法求解。
2. 确定状态和状态变量：将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来。当然，状态的选择要满足无后效性。
3. 确定决策并写出状态转移方程：因为决策和状态转移有着天然的联系，状态转移就是根据上一阶段的状态和决策来导出本阶段的状态。所以如果确定了决策，状态转移方程也就可写出。但事实上常常是反过来做，根据相邻两个阶段的状态之间的关系来确定决策方法和状态转移方程。
4. 寻找边界条件：给出的状态转移方程是一个递推式，需要一个递推的终止条件或边界条件。

涉及题目

LeetCode-918. 环形子数组的最大和

LeetCode-1567. 乘积为正数的最长子数组长度

LeetCode-122. 买卖股票的最佳时机 II

LeetCode-62. 不同路径

LeetCode-64. 最小路径和