排序算法- 八大排序

排序算法有：冒泡、选择、插入、希尔、归并、快速、堆、基数、计数

冒泡

白话：像水中的气泡一样，一次出一个最大的数出来。 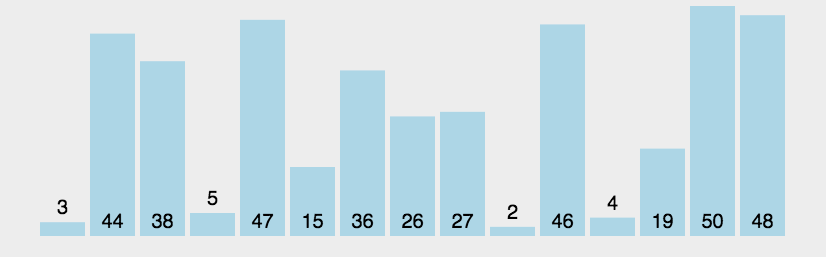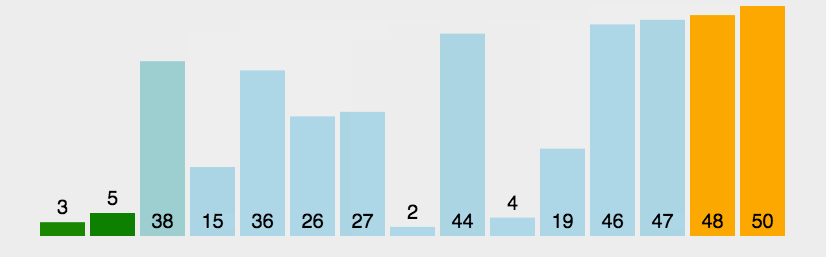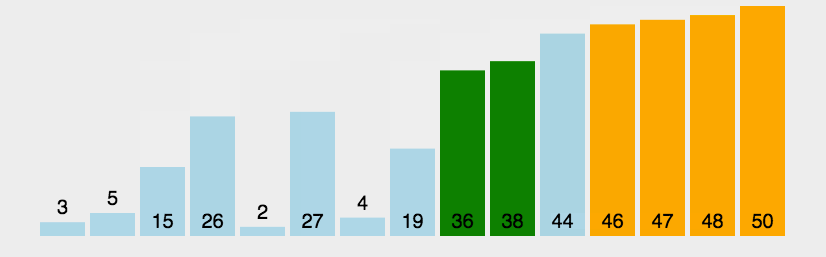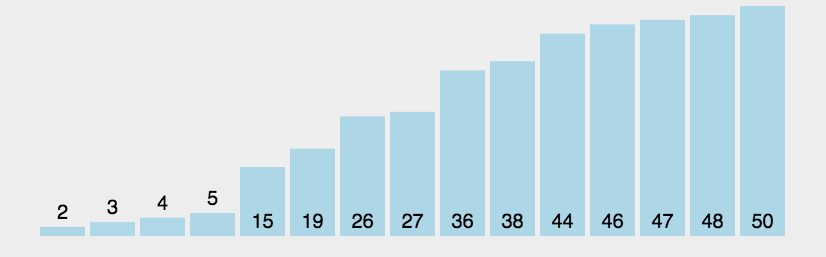评价：不好用，无论如何进行优化就无法降低其时间复杂的问题，所以也极其稳定的保证在O(n^2)上。 代码:

    public static void main (String[] args) {
        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr.length - i - 1; j++) {
                if (arr[j + 1] < arr[j]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
        SystemArray.systemArr(arr);
    }


    //优化方案
    public void test2 () {
        for (int i = 0; i < arr.length; i++) {
            boolean is = true;
            for(int j=0;j<arr.length-1-i;j++){
                if(arr[j+1]<arr[j]){
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                    is=false;
                }
            }
            if(is){
                break;
            }
        }
    }

选择

白话：默认选择第一个为当前数组最小，并且记录位置。将当前最小数的位置与其他数进行比较，找到数组中最小的数。交换两者下标。 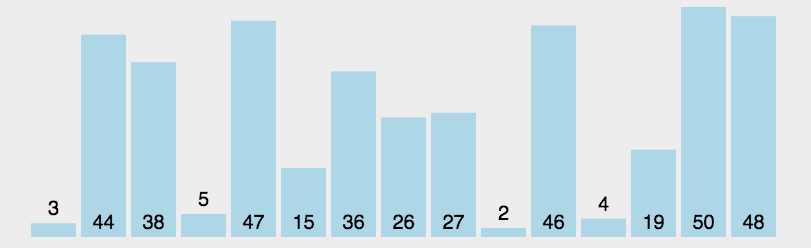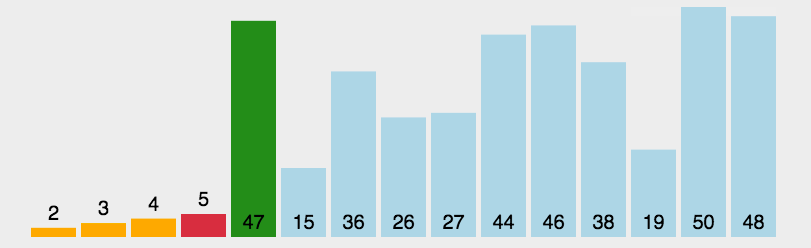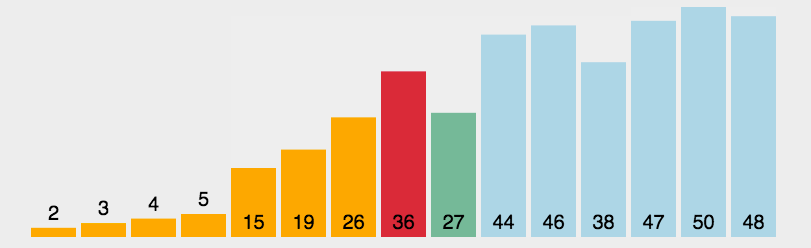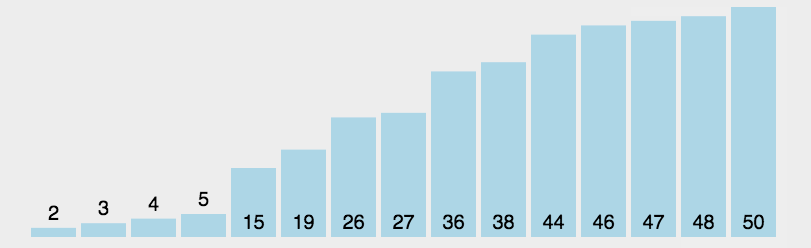评价：很难的一种排序方法，原理上和冒泡一样，都是通过双循环，确定每个元素在数组中的位置。但是无论原数组是怎样的顺序，都会进行双循环且每个元素之间进行判断。 代码：

    public static void main (String[] args) {
        for(int i=0;i<arr.length;i++){
            int index = i;
            for(int j=i;j<arr.length;j++){
                if(arr[index]>arr[j]){
                    index= j ;
                }
            }
            if(index!=i){
                int temp = arr[i];
                arr[i] = arr[index];
                arr[index] = temp;
            }
        }
        SystemArray.systemArr(arr);
    }

插入

白话：动态的控制前N的数组列为有序数组，当遍历到下一元素时，只需要不断的与该有序数组的最大值进行比较，直到找到比新值小的数出现。插入到这个数前面。 评价：由于会动态的去维护一个有序数组列，所以在实际开发中优先于冒泡。当业务需要时，可以随时中断排序，只取当前有序数组列。所以在开发中比较灵活 代码：

    public static void main(String[] args) {
        for (int i = 0; i < arr.length - 1; i++) {
            int temp = arr[i + 1];
            int index = i;
            while (index >= 0 && arr[index] > temp) {
                arr[index+1] = arr[index]; 
                index--;
            }
            if(index!=i){
                arr[index+1] = temp;
            }
        }
        SystemArray.systemArr(arr);
    }

归并

白话：将一个数组，拆分成最小单位1的数组。但是在单位为2的数组时进行两两判断；所以使用迭代的手法，将数组不断的分隔为两半，左left和右left。并且将两数组通过合并排序，得到新的数组，返回出去。 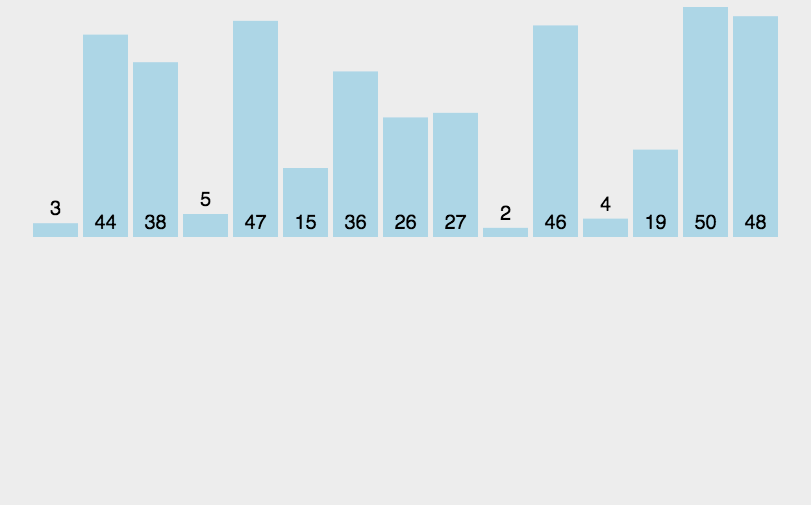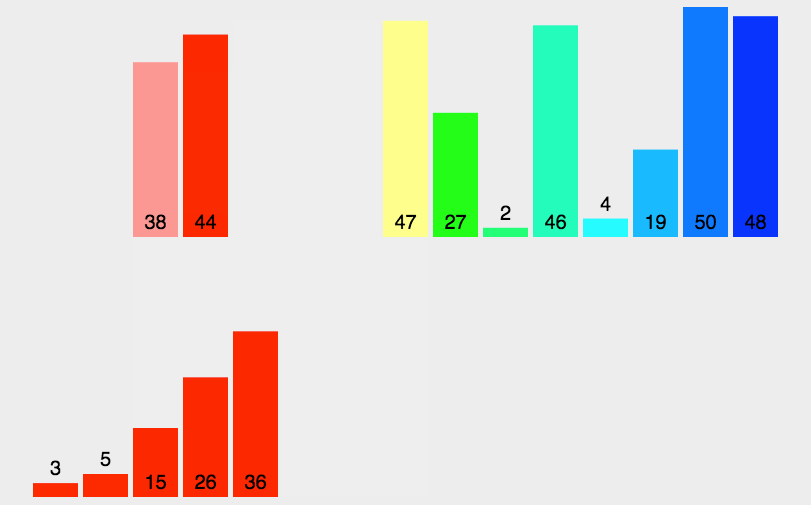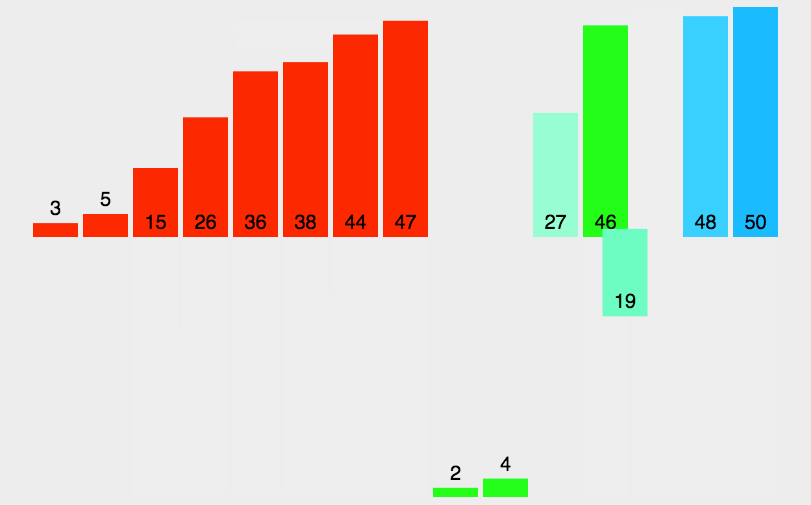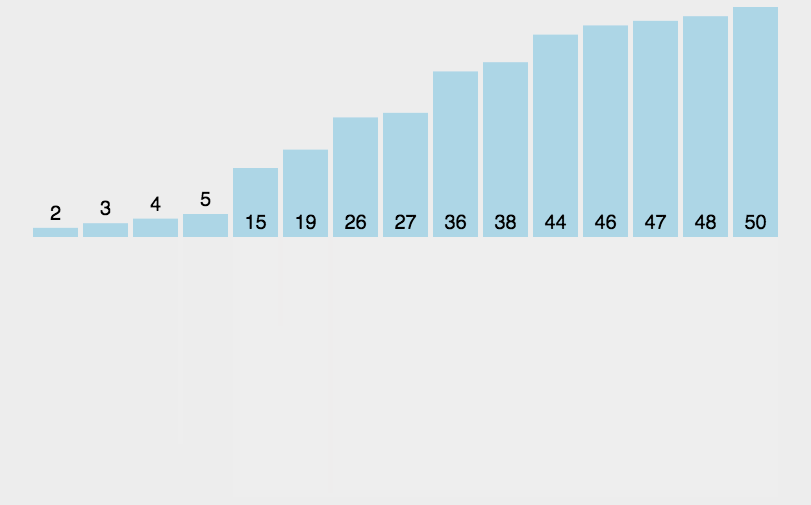评价：使用的分治的手段，带来了迭代。所以空间消耗上不断的消耗新数组空间，但由于/2的拆分数组，所以避免的空判断的形式。时间上减少了很多。 代码：

    public static void main(String[] args) {
        int[] arr = {4, 2, 5, 7, 3, 6, 10, 1};
        int[] ints = mergetSort(arr);
        SystemArray.systemArr(arr);
    }

    public static int[] mergetSort(int[] arrs) {
        if (arrs.length < 2) {
            return arrs;
        }
        int mid = arrs.length / 2;
        int left[] = Arrays.copyOfRange(arrs, 0, mid);
        int right[] = Arrays.copyOfRange(arrs, mid, arrs.length);
        return merget(mergetSort(left), mergetSort(right));
    }

    public static int[] merget(int[] left, int[] right) {
        int result[] = new int[left.length + right.length];
        for (int index = 0, l = 0, r = 0; index < result.length; index++) {
            if (r>=left.length) {
                result[index] = left[l++];
            } else if (l>=right.length) {
                result[index] = right[r++];
            } else if (left[l] > right[r]) {
                result[index] = right[r++];
            } else {
                result[index] = left[l++];
            }
        }
        return result;
    }

快速排序

白话：选一个数，一般默认选坐标0-left。设置right坐标，遍历数组，将right从右往左扫描，当遇到比坐标0temp值小的，放到temp值左边，即与left交换。交替扫描，切换到left从左往右扫描，知道找到比temp值大的，放到temp值右边，即与right坐标进行交换。直到left和right重合，此时temp左边都是小于他的，右边是大于他的。然后将他的右边和左边分别进行单独的排序，直到单位数组为1时结束。 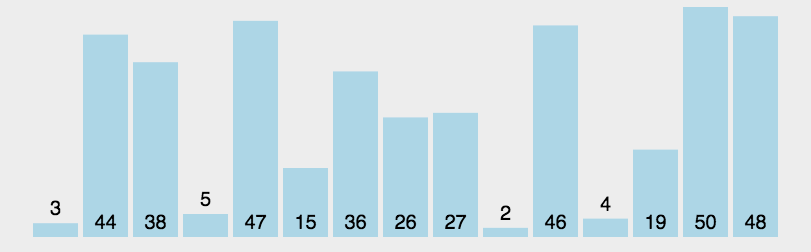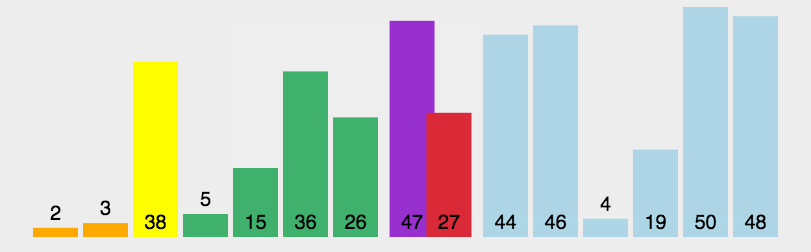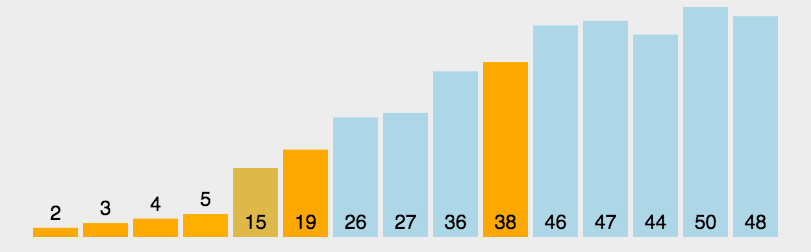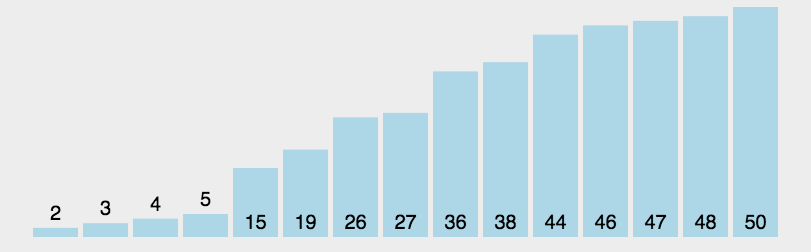评价：极其不稳定的算法，如名字所示，我只管快，会怎样我不管。所以在最坏的情况下，数组完全无序。左右指针需要交替的走完全程交换。 代码:

    public static void main(String[] args) {

        quickSort(0,arr.length-1,arr);
        SystemArray.systemArr(arr);
    }

    public static void quickSort(int start,int end,int [] arrs){
        if(end>start && start>=0 && end<=arr.length-1){
            int quick = quick(start, end, arrs);
            quickSort(start,quick-1,arrs);
            quickSort(quick+1,end,arrs);
        }
    }
    
    public static int quick(int start,int end,int [] arrs){
        int left=start;
        int right=end;
        int temp = arrs[left];
        while(left!=right){
            while(arrs[right]>temp && right>left){
                right--;
            }
            arrs[left] = arrs[right];
            while(arrs[left]<temp && left<right){
                left++;
            }
            arrs[right] = arrs[left];
        }
        arrs[right] = temp;
        return right;
    }

堆

白话：将数组按顺序打在二叉树上，将每个叶子 [叶子节点和根]看成一个堆。维护每个堆的最大堆概念，即根节点为最大值。这时候，根节点就是数组的最大值，且其叶子节点都是余下节点的最大值。所以只需要将根节点与最远节点进行交换，并且不断维护最大堆概念。就可以得到一个有序数组了。 评价：不稳定的排序，会将所有的原数组值都进行替换。并且在代码层面不够直观理解，除了时间消耗底，空间消耗低外，你一无是处。 代码:

    public static void main (String[] args) {
        heapSort();
        int len = arr.length;
        while(len>0){
            int temp=arr[0];
            arr[0] = arr[len-1];
            arr[len-1] = temp;
            getMaxHeap(arr,0);
            len--;
        }
        SystemArray.systemArr(arr);
    }

    public static void heapSort(){
        for(int i = (arr.length-1)/2 ; i>=0;i--){
            getMaxHeap(arr,i);
        }
    }

    public static void getMaxHeap (int[] arrs, int i) {
        int temp = i;
        if (i * 2 < arrs.length && arrs[i * 2] > arrs[temp]) {
            temp = i*2;
        }
        if (i * 2 + 1 < arrs.length && arrs[i * 2 + 1] > arrs[temp]) {
            temp = i*2+1;
        }
        if(temp != i ){
            int num = arrs[i];
            arrs[i] = arrs[temp];
            arrs[temp] = num;

            getMaxHeap(arrs,temp);
        }
    }

计数

白话：没有比较过程，通过创建原数组最大值长度的数组。然后将数组的值与新数组下标进行累加匹配。最后遍历新数组，从左往后，找到有记录的值则说明这个值就是最小值。 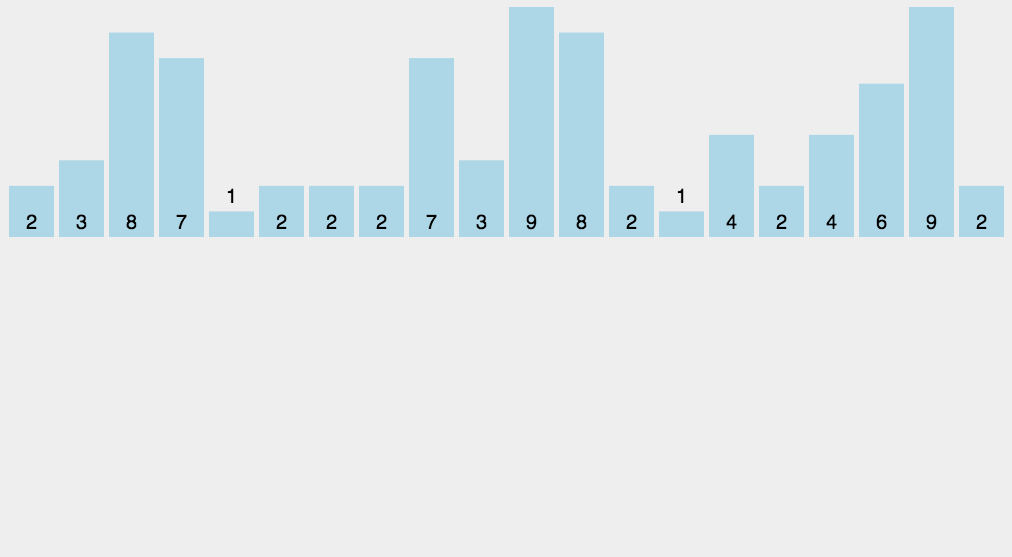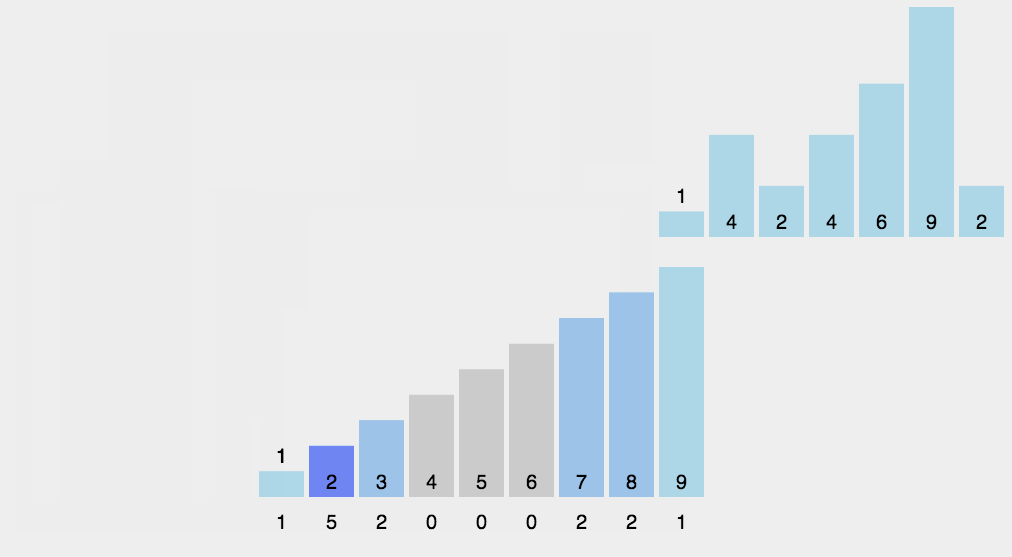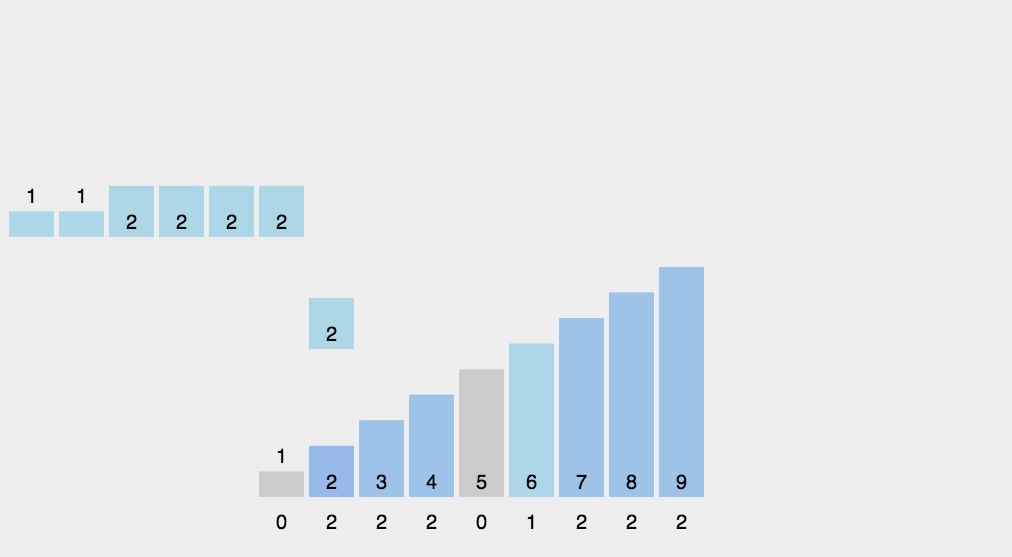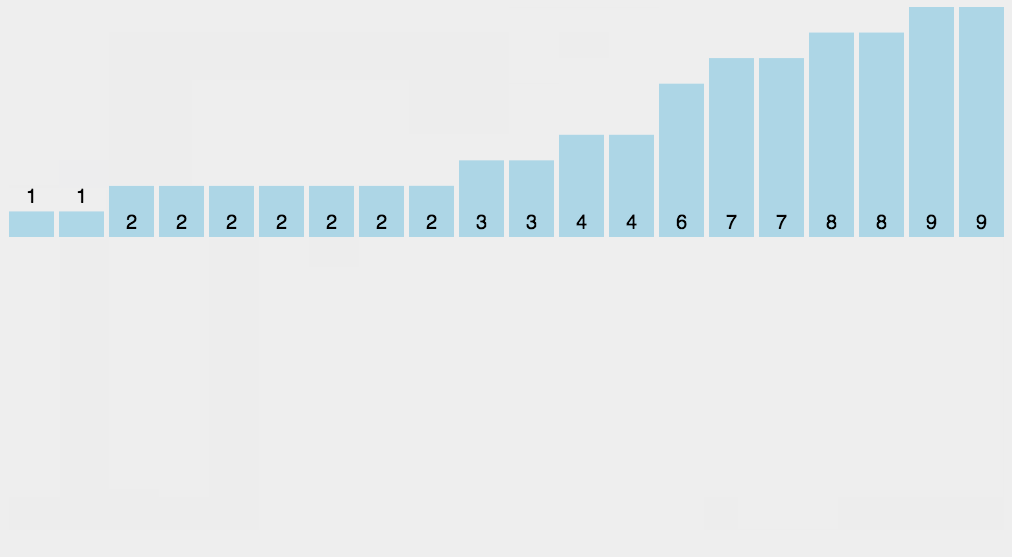评价：没有数与数之间比较的线性排序，其性能完全由数组中最大值判断。与其说排序，其实在计数的业务场景中见的更多 代码:

    public static void main (String[] args) {
        int max = 0;
        for(int i :arr){
            if(i>max){
                max = i;
            }
        }
        int [] bucket=new int [max+1];
        Arrays.fill(bucket,0);
        for(int i:arr){
            bucket[i]++;
        }
        int index = 0;
        int i= 0;
        while(index<arr.length){
            if(bucket[i]!=0){
                arr[index] = i;
                bucket[i]--;
                index++;
            }else{
                i++;
            }
        }
        SystemArray.systemArr(arr);
    }