LeetCode-1685. 有序数组中差绝对值之和

示例 1：

输入：nums = [2,3,5]
输出：[4,3,5]
解释：假设数组下标从 0 开始，那么
result[0] = |2-2| + |2-3| + |2-5| = 0 + 1 + 3 = 4，
result[1] = |3-2| + |3-3| + |3-5| = 1 + 0 + 2 = 3，
result[2] = |5-2| + |5-3| + |5-5| = 3 + 2 + 0 = 5。

示例 2：

输入：nums = [1,4,6,8,10]
输出：[24,15,13,15,21]

解题思路

审题，涉及到数组计算，第一反应就是去找规律公式。 如示例2中 对于nums[2]而言 有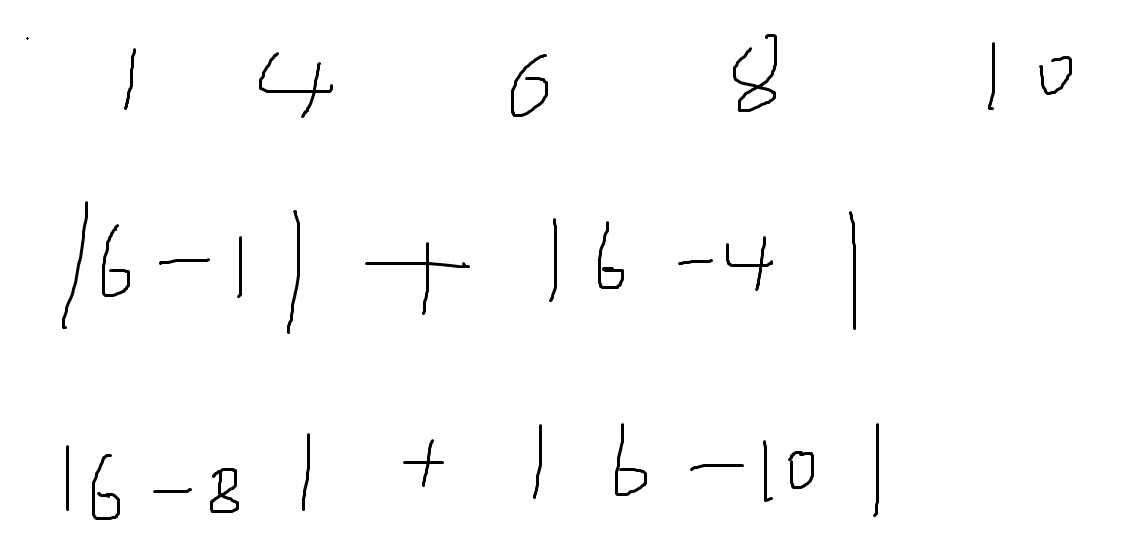： 因为题目里有说数组为递增的有序数组，result里的值为绝对值结果 可以看出从nums[2]往前为nums[2] -nums[1] .....往后为nums[3]-nums[2]...nums[4]-nums[2] 所以可以公式可以在往细划分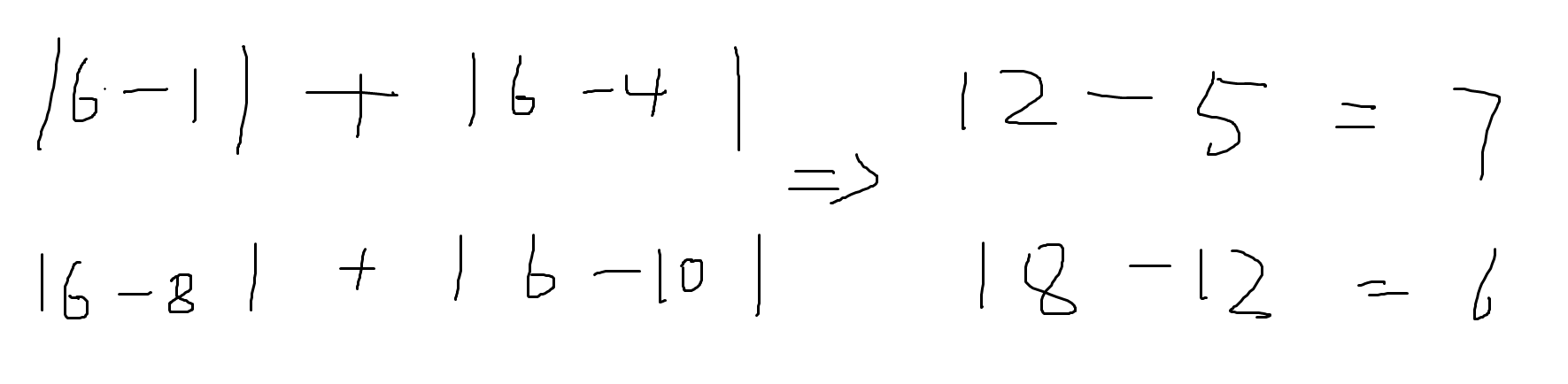

这样写出来可以看出，result[2]的值可以当做以nums[2]为分界线；前缀和以及后缀和计算出的结果. 设preSum为前缀和，sufSum为后缀和. 则result[2]=2nums[2]-preSum+sufSum-(2nums[2])

所以解题的关键点就是求出前缀和和后缀和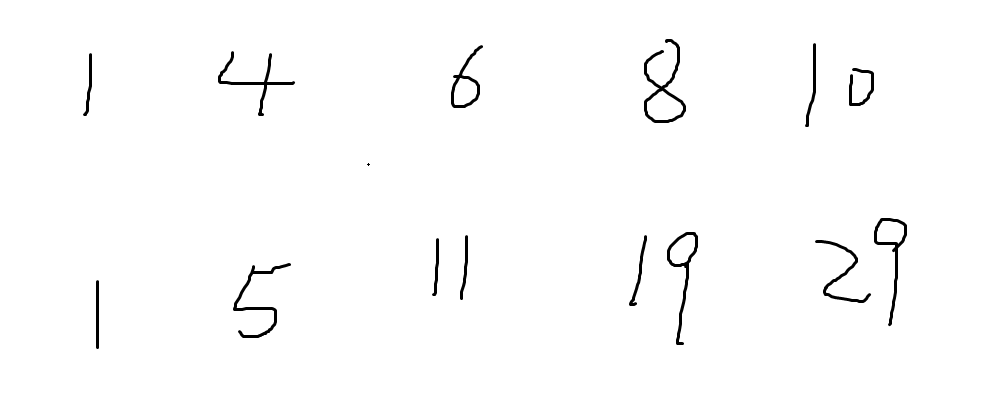 列出当前的所有数组下标对应的前缀和. 这样若以6->nums[2]为例，前缀和就是5 ，后缀就是29-11=18. 最后将思路转换成代码就可以得出

代码

public static int[] getSumAbsoluteDifferences(int[] nums) {
        int len=nums.length;
        int [] result=new int[len];
        int [] preSum=new int [len];
        int sum=0;
        for(int i=0;i<len;i++){
            sum+=nums[i];
            preSum[i]=sum;
        }
        int sufSum=0; //后缀和
        for(int i=0;i<len;i++){
            sufSum=preSum[len-1]-preSum[i];
            result[i]=(sufSum-(len-1-i)*nums[i])+((i+1)*nums[i]-preSum[i]);
        }
        return result;
    }

失败例子

最开始的代码和思路，结果没错，但是时间复杂度怪怪的，所以一直超时。主要是没想到算所有数组下标对应的总和来以此计算。

public static int[] getSumAbsoluteDifferences(int[] nums) {
        int [] result=new int [nums.length];
        int index=0; //当前下标
        int pre=0; //前缀下标
        int preSum=0; //前缀和
        int sufSum=0; //后缀和
        while(index!=nums.length){
            int suf=index+1; //后缀下标
            while(pre!=index || suf!=nums.length){
                if(pre<index){
                    preSum+=nums[pre]; //前缀和
                    pre++;
                }
                if(suf<=nums.length-1){
                    sufSum+=nums[suf]; //后缀和
                    suf++;
                }
            }
            int sufCount=nums.length-1-index;
            result[index]=(sufSum-sufCount*nums[index])+(index*nums[index]-preSum);
            suf=0;
            pre=0;
            index++;
        }
        return result;
    }