LeetCode-20. 有效的括号和其拓展逆波兰式

示例 2：

输入：s = "()[]{}"
输出：true

思路

括号匹配是很简单的单调栈的应用，通过栈操作栈顶的特性，可以保证栈顶元素和循环字符串的元素匹配的真实性。

代码

    public static boolean isValid(String s) {
        if(s.length()==2){
            return s.equals("()")||s.equals("{}")||s.equals("[]");
        }
        if(s.length()%2!=0){
            return false;
        }
        Stack<Character> stack=new Stack<>();
        Map<Character,Character> map=new HashMap<>();
        map.put(')','(');
        map.put('}','{');
        map.put(']','[');
        for(int i=0;i<s.length();i++){
            char c = s.charAt(i);
            if(null==map.get(c)){
                stack.push(c);
            }else{
                if(stack.empty() || stack.pop().charValue()!=map.get(c)){
                   return false;
                }
            }
        }
        return stack.empty();
    }

拓展

如果说括号匹配是很简单的单调栈的应用，那么以此思路为头。 可以想到逆波兰表达式的算法表达思路

逆波兰表达式

波兰表达式，学名后缀表达式。 而我们平时使用的数学计算表达式为中缀表达式。 例如：

（3+4）5-6 -> 34+56-

按照这样的表达式出的结果，虽然以人的角度比较难理解，但是计算机的计算过程中，就是使用后缀表达式为基础计算的。 所以有必要去了解这种表达式。

作用

由于计算机普通采用的内存结构是栈，基于先进后出的原理，如果以此来理解我们日常生活中的中缀表达式，计算机是无法计算的。 所以在数据结构中，为计算机提供了容易解析的后缀表达式。

算法

既然涉及到了数据结构，那么从中缀表达式转换为后缀表达式就是我们必须去理解的过程。 不同于本文的括号匹配，在表达式的转换过程中。因为计算符号的优先级、特殊符号的优先级的影响。在转换过程中，还需要使用一个栈作为存储栈来划分各优先级计算的顺序。

算法的实现，网络上有很多教程

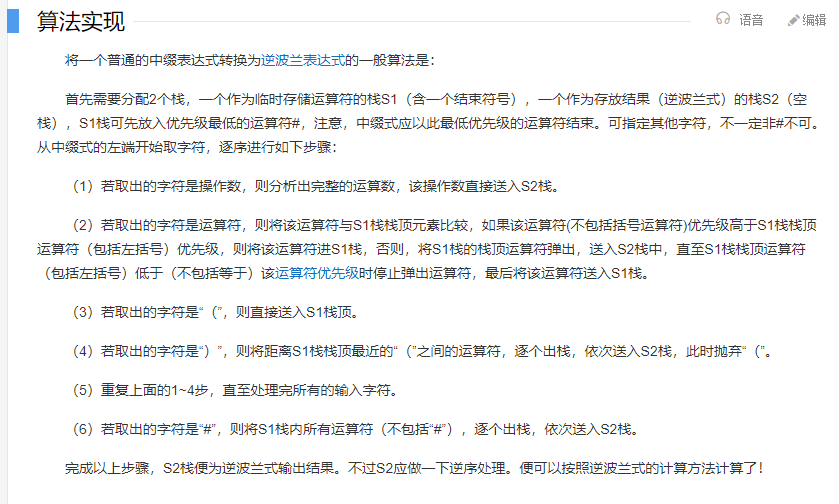
这是最常用的思路，不难，就是循环遍历字符串的过程中，判断其是否是数字或是操作符，然后将其压入对应栈里进行判断。 不过在只是翻译的前提下，我推荐使用括号法。

括号法

出自：CSDN-中缀表达式转后缀表达式